
Statistikk: ANOVAI analysene så langt har vi stilt nokså "enkle" spørsmål, og fått nokså "enkle" svar. Men verden (og våre spørsmål) er ofte mer komplekse! La oss ta utgangspunkt i datafilen fra tidligere. Her har vi sammenlignet to grupper elever som har gjennomgått sosial trening (ART) eller ikke (KONTRL). Dette vil altså være en uavhengig variabel (eller faktor) i denne undersøkelsen. Elevene ble tilfeldig fordelt til betingelsene. Avhengig variabel er målt sosial kompetanse etter intervensjon; skårer for dette ses i variabelen KOMP2. Samtidig inneholder datafilen en annen uavhengig variabel (faktor), nemlig kjønn - både gutter og jenter har deltatt i begge gruppene:
Samtidig inneholder datafilen en annen uavhengig variabel (faktor), nemlig kjønn - både gutter og jenter har deltatt i begge gruppene:
 Dette tillater oss å stille følgende litt mer komplekse spørsmål: Hva betyr intervensjon (ART vs. kontroll) for sosial kompetanse, og hva betyr kjønn? Denne analysen tillater altså at vi i samme test undersøker effekten av to uavhengige variabler. Tester vi tidligere har omtalt kan bare undersøke effekten av en uavhengig variabel om gangen. Ved bruk av ANOVA (variansanalyse; Analysis of Variance) kan vi altså spørre mer nyansert. I dette eksemplet undersøker vi altså effekten av to uavhengige variabler i samme test.
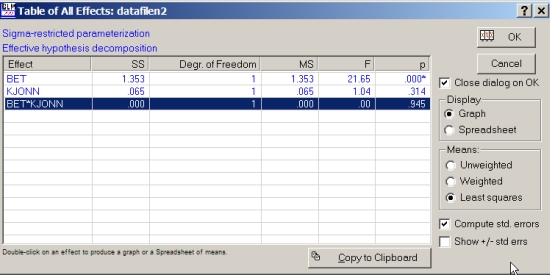
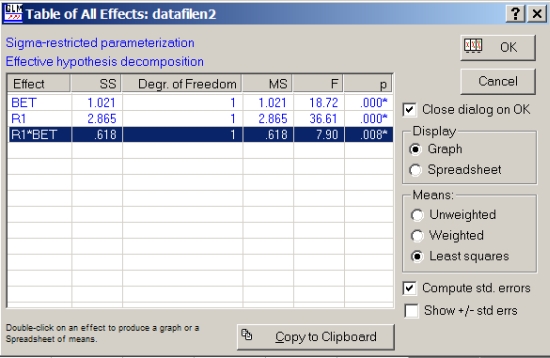
I utskriften under ses utfallet. ANOVA tester om noen av de to manipulerte faktorene (betingelse - ART vs. kontroll; kjønn) kan forklare variasjon observert i den avhengige variabelen, KOMP2. Svaret ses i utskriften i form av F-verdien (kolonnen nest lengst til høyre). Jo høyere F-verdi, desto mer variasjon i den avhengige variabelen forklares av den manipulerte faktoren. I dette eksemplet ser vi at BET har en høy F-verdi (21,65), mens kjønn har en lav F-verdi (1,04). Det er dermed svært usannsynlig at den første skulle ha oppstått tilfeldig (se p-verdien i kolonnen lengst ute til høyre!); motsatt er F-verdien for kjønn så liten at variasjonen assosiert med kjønn godt kan være tilfeldig.
Dette tillater oss å stille følgende litt mer komplekse spørsmål: Hva betyr intervensjon (ART vs. kontroll) for sosial kompetanse, og hva betyr kjønn? Denne analysen tillater altså at vi i samme test undersøker effekten av to uavhengige variabler. Tester vi tidligere har omtalt kan bare undersøke effekten av en uavhengig variabel om gangen. Ved bruk av ANOVA (variansanalyse; Analysis of Variance) kan vi altså spørre mer nyansert. I dette eksemplet undersøker vi altså effekten av to uavhengige variabler i samme test.
I utskriften under ses utfallet. ANOVA tester om noen av de to manipulerte faktorene (betingelse - ART vs. kontroll; kjønn) kan forklare variasjon observert i den avhengige variabelen, KOMP2. Svaret ses i utskriften i form av F-verdien (kolonnen nest lengst til høyre). Jo høyere F-verdi, desto mer variasjon i den avhengige variabelen forklares av den manipulerte faktoren. I dette eksemplet ser vi at BET har en høy F-verdi (21,65), mens kjønn har en lav F-verdi (1,04). Det er dermed svært usannsynlig at den første skulle ha oppstått tilfeldig (se p-verdien i kolonnen lengst ute til høyre!); motsatt er F-verdien for kjønn så liten at variasjonen assosiert med kjønn godt kan være tilfeldig.
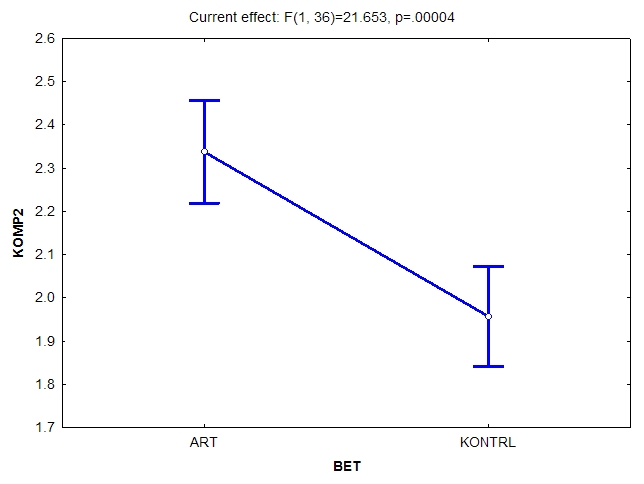
 Den første effekten illustreres i følgende graf. Merk at F-verdien bare sier at et er en systematisk effekt; grafen viser hvordan den ser ut.
Den første effekten illustreres i følgende graf. Merk at F-verdien bare sier at et er en systematisk effekt; grafen viser hvordan den ser ut.
 Det er ingen signifikant effekt av kjønn, men la oss likevel se hvordan bildet ser ut (strengt tatt er det bare "lov" å vise figur av signifikante effekter):
Det er ingen signifikant effekt av kjønn, men la oss likevel se hvordan bildet ser ut (strengt tatt er det bare "lov" å vise figur av signifikante effekter):
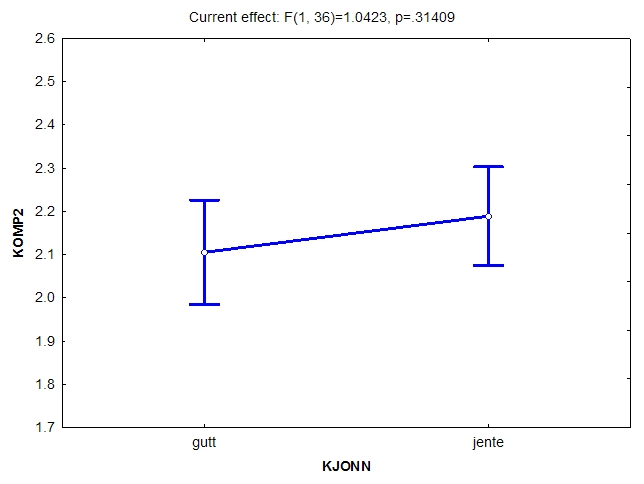 Disse to figurene illustrerer den generelle effekten av de to manipulerte variablene, dvs. hovedeffektene av disse variablene. Men ANOVA tillater ytterligere en analyse, nærmere bestemt av effekten av de to manipulerte variablene sammen. Her spør vi: Har det noen betydning for intervensjonen (ART vs. KONTRL) hvilket kjønn eleven har? Hvis det har det, snakker vi om en samspillseffekt eller interaksjonseffekt.
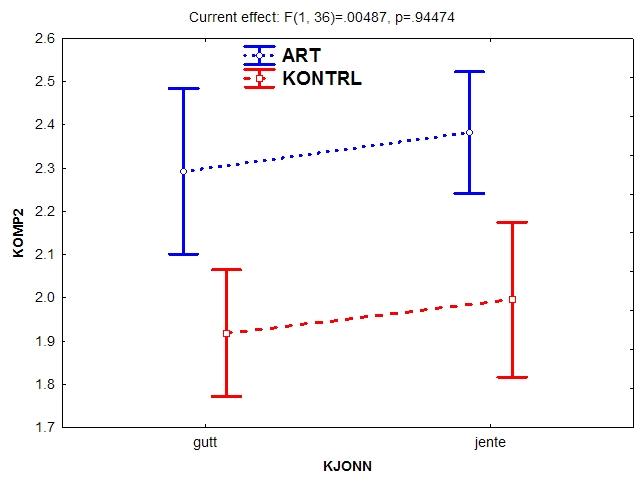
Svaret på dette spørsmålet ses i siste linje av utskriften, nemlig effekten BET*KJONN. Som det fremgår av utskriften, er F-verdien assosiert med interaksjonen 0. Dette betyr at kjønn ikke har noen som helst betydning for effekten av intervensjonen. Dette illustreres i figuren under. Merk at de stiplede linjene er helt parallelle. Dette indikerer fravær av en interaksjon. Intervensjonen har dermed samme effekt for både gutter og jenter.
Disse to figurene illustrerer den generelle effekten av de to manipulerte variablene, dvs. hovedeffektene av disse variablene. Men ANOVA tillater ytterligere en analyse, nærmere bestemt av effekten av de to manipulerte variablene sammen. Her spør vi: Har det noen betydning for intervensjonen (ART vs. KONTRL) hvilket kjønn eleven har? Hvis det har det, snakker vi om en samspillseffekt eller interaksjonseffekt.
Svaret på dette spørsmålet ses i siste linje av utskriften, nemlig effekten BET*KJONN. Som det fremgår av utskriften, er F-verdien assosiert med interaksjonen 0. Dette betyr at kjønn ikke har noen som helst betydning for effekten av intervensjonen. Dette illustreres i figuren under. Merk at de stiplede linjene er helt parallelle. Dette indikerer fravær av en interaksjon. Intervensjonen har dermed samme effekt for både gutter og jenter.
 Hvis du tar en titt på datafilen øverst på siden, ser du at vi faktisk har to mål på sosial kompetanse, KOMP og KOMP2. Det første er et mål vi innhenter før intervensjonen, det andre ble innhentet etter intervensjonen. ANOVA tillater en analyse hvor disse før- og etter-målene sammenlignes. Vi har to bestemte forventninger til disse dataene: (1) Før intervensjon skal det ikke være noen forskjell mellom gruppene (deltakerne ble jo tilfeldig fordelt til betingelsene); (2) Etter intervensjonen skal det være en forskjel ved at ART-gruppen øker sin kompetanse, mens kontrollgruppen ikke gjør det. Dette er altså en forventning om en interaksjonseffekt, R1*BET ("R1" viser til den repeterte målingen av sosial kompetanse før og etter intervensjon, KOMP og KOMP2).
La oss se på resultatene. Utskriften under tilsier at hver av de manipulerte variablene har hatt effekt:
Hvis du tar en titt på datafilen øverst på siden, ser du at vi faktisk har to mål på sosial kompetanse, KOMP og KOMP2. Det første er et mål vi innhenter før intervensjonen, det andre ble innhentet etter intervensjonen. ANOVA tillater en analyse hvor disse før- og etter-målene sammenlignes. Vi har to bestemte forventninger til disse dataene: (1) Før intervensjon skal det ikke være noen forskjell mellom gruppene (deltakerne ble jo tilfeldig fordelt til betingelsene); (2) Etter intervensjonen skal det være en forskjel ved at ART-gruppen øker sin kompetanse, mens kontrollgruppen ikke gjør det. Dette er altså en forventning om en interaksjonseffekt, R1*BET ("R1" viser til den repeterte målingen av sosial kompetanse før og etter intervensjon, KOMP og KOMP2).
La oss se på resultatene. Utskriften under tilsier at hver av de manipulerte variablene har hatt effekt:
 Den tredje av disse, den forventede interaksjonseffekten, ser slik ut:
Den tredje av disse, den forventede interaksjonseffekten, ser slik ut:
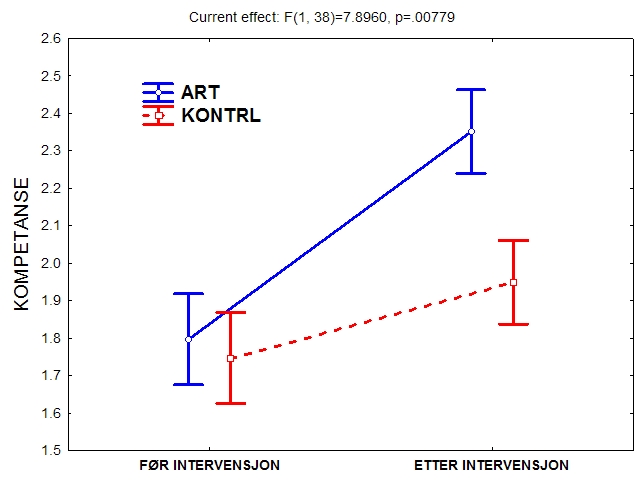 Grafen er enkel å tolke: (1) Før intervensjon var det ikke noen forskjell mellom gruppene, slik vi predikerte; (2) Etter intervensjonen var det en forskjell ved at ART-gruppen åpnbart viste en høyere skåre på sosiale ferdigheter enn kontrollgruppen. Merk at linjene ikke er parallelle, noe som altså kjennetegner interaksjonseffekter.
Grafen er enkel å tolke: (1) Før intervensjon var det ikke noen forskjell mellom gruppene, slik vi predikerte; (2) Etter intervensjonen var det en forskjell ved at ART-gruppen åpnbart viste en høyere skåre på sosiale ferdigheter enn kontrollgruppen. Merk at linjene ikke er parallelle, noe som altså kjennetegner interaksjonseffekter.
I disse analysene har vi undersøkt affektene av to manipulerte faktorer, intervensjon og kjønn, på en avhengig variabel (sosial kompetanse etter intervensjon). ANOVA har imidlertid et mye større bruksområde. Eksempler:
 Tilbake Tilbake
|